Static Analysis of Uncertain Structures
| ✅ Paper Type: Free Essay | ✅ Subject: Engineering |
| ✅ Wordcount: 2962 words | ✅ Published: 31 Aug 2017 |
Static Analysis of Uncertain Structures Using Interval Eigenvalue Decomposition
1Mehdi Modares and 2Robert L. Mullen
1Department of Civil and Environmental
Engineering
Tufts University
Medford, MA, 02155
2Department of Civil Engineering
Case Western Reserve University
Cleveland, OH, 44106
Abstract: Static analysis is an essential procedure to design a structure. Using static analysis, the structure’s response to the applied external forces is obtained. This response includes internal forces/moments and internal stresses that is used in the design process. However, the mechanical characteristics of the structure possess uncertainties which alter the structure’s response. One method to quantify the presence of these uncertainties is interval or unknown-but-bounded variables.
In this work a new method is developed to obtain the bounds on structure’s static response using interval eigenvalue decomposition of the stiffness matrix. The bounds of eigenvalues are obtained using monotonic behavior of eigenvalues for a symmetric matrix subjected to non-negative definite perturbations. Moreover, the bounds of eigenvectors are obtained using perturbation of invariant subspaces for symmetric matrices. Comparisons with other interval finite element solution methods are presented. Using this method, it has shown that obtaining the bound on static response of an uncertain structure does not require a combinatorial or Monte-Carlo simulation procedure.
Keywords: Statics, Analysis, Interval, Uncertainty
© 2008 by authors. Printed in USA.
REC 2008 – Modares and Mullen
In design of structures, the performance of the structure must be guaranteed over its lifetime. Moreover, static analysis is a fundamental procedure for designing reliable structure that are subjected to static or quasi-static forces induced by various loading conditions and patterns.
However, in current procedures for static analysis of structural systems, the existence of uncertainty in either mechanical properties of the system or the characteristics of forcing function is generally not considered. These uncertainties can be attributed to physical imperfections, modeling inaccuracies and system complexities.
Although, in a design process, uncertainty is accounted for by a combination of load amplification and strength reduction factors that are based on probabilistic models of historic data, consideration of the effects of uncertainty has been removed from current static analysis of structural systems.
In this work, a new method is developed to perform static analysis of a structural system in the presence of uncertainty in the system’s mechanical properties as well as uncertainty in the magnitude of loads. The presence of these uncertainties is quantified using interval or unknownbut-bounded variables.
This method obtains the bounds on structure’s static response using interval eigenvalue decomposition of the stiffness matrix. The bounds of eigenvalues are obtained using the concept of monotonic behavior of eigenvalues for a symmetric matrix subjected to non-negative definite perturbations. Furthermore, the bounds of eigenvectors are obtained using perturbation of invariant subspaces for symmetric matrices. Using this method, it has shown that obtaining the bound on static response of an uncertain structure does not require a combinatorial or MonteCarlo simulation procedure.
The equation of equilibrium for a multiple degree of freedom structure is defined as a linear system of equations as:
[K]{U}={P} (1)
where, [K]is the stiffness matrix, {U}is the vector of unknown nodal displacements, and {P} is the vector of nodal forces. The solution to this system of equation is:
{U} = [K]−1{P} (2)
The concept of interval numbers has been originally applied in the error analysis associated with digital computing. Quantification of the uncertainties introduced by truncation of real numbers in numerical methods was the primary application of interval methods (Moore 1966).
A real interval is a closed set defined by extreme values as (Figure 1):
~l ,zu ] ={z∈ℜ| zl ≤ z ≤ zu} (3)
Z = [z

~
x = [a,b]
Figure 1. An interval variable.
In this work, the symbol (~) represents an interval quantity. One interpretation of an interval number is a random variable whose probability density function is unknown but non-zero only in the range of interval.
Another interpretation of an interval number includes intervals of confidence for α-cuts of fuzzy sets. The interval representation transforms the point values in the deterministic system to inclusive set values in the system with bounded uncertainty.
Considering the presence of interval uncertainty in stiffness and force properties, the system of equilibrium equations, Eq.(1), is modified as an interval system of equilibrium equation as:
~~
[K]{U}={P} (4)
~
where, [K]is the interval stiffness matrix, {U}is the vector of unknown nodal displacements, and {P} is the vector of interval nodal forces. In development of interval stiffness matrix, the physical and mathematical characteristics of the stiffness matrix must be preserves.
This system of interval equations is mainly solved using computationally iterative procedures (Muhanna et al 2007) and (Neumaier and Pownuk 2007). The present method proposes a computationally efficient procedure with nearly sharp results using interval eigenvalue decomposition of stiffness matrix.
While the external force can also have uncertainties, in this work only problems with interval stiffness properties are addressed. However, for functional independent variations for both stiffness matrix and external force vector, the extension of the proposed work is straightforward.
3.1. DETERMINISTIC EIGENVALUE DECOMPOSITION
The deterministic symmetric stiffness matrix can be decomposed using matrix eigenvalue decomposition as:
[K] = [Φ][Λ][Φ]T (5)
where, [Φ] is the matrix of eigenvectors, and [Λ] is the diagonal matrix of eigenvalues. Equivalently,
N
[K] =∑λi{Ï•i}{Ï•i}T (6)
i=1
where, the values of λi is the eigenvalues and the vectors{Ï•i}are their corresponding eigenvectors. Therefore, the eigenvalue decomposition of the inverse of the stiffness matrix is:
|
equivalently, |
[K]−1 =[Φ][Λ]−1[Φ]T |
(7) |
|
−N 1T [K] 1 =∑ |
(8) |
i=1 λi
Substituting Eq.(8) in the solution for the deterministic linear system of equation, Eq.(2), the solution for response is shown as:
{U}= (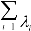 N
N  1 {Ï•i}{Ï•i}T ){P} (9)
1 {Ï•i}{Ï•i}T ){P} (9)
3.2. INTERVAL EIGENVALUE DECOMPOSITION
Similarly, the solution to interval system of equilibrium equations, Eq.(4), is:
{U~}= (∑N ~1 {Ï•~ }{Ï•~i}T ){P} (10) i
i=1 λi
~~ } are their where, the values of λi is the interval eigenvalues and, the vectors {Ï•i
corresponding interval eigenvectors that are to be determined.
4.1. BACKGROUND
The research in interval eigenvalue problem began to emerge as its applicability in science and engineering was realized. Hollot and Bartlett (1987) studied the spectra of eigenvalues of an interval matrix family which are found to depend on the spectrum of its extreme sets. Dief (1991) presented a method for computing interval eigenvalues of an interval matrix based on an assumption of invariance properties of eigenvectors.
In structural dynamics, Modares and Mullen (2004) have introduced a method for the solution of the interval eigenvalue problem which determines the exact bounds of the natural frequencies of a system using Interval Finite Element formulation.
4.2. DEFINITION
The eigenvalue problems for matrices containing interval values are known as the interval
~ ~ n–n ) and [A] is a member of the eigenvalue problems. If [A] is an interval real matrix (A∈ℜ
~
interval matrix ([A]∈[A]) , the interval eigenvalue problem is shown as:
~
4.2.1. Solution for Eigenvalues
The solution of interest to the real interval eigenvalue problem for bounds on each eigenvalue is
~
defined as an inclusive set of real values (λ) such that for any member of the interval matrix, the eigenvalue solution to the problem is a member of the solution set. Therefore, the solution to the interval eigenvalue problem for each eigenvalue can be mathematically expressed as:
~l ,λu ]|∀[A]∈[A~]: ([A]−λ[I]){x} = 0} (12)
{λ∈λ= [λ
4.2.2. Solution for Eigenvectors:
The solution of interest to the real interval eigenvalue problem for bounds on each eigenvector is defined as an inclusive set of real values of vector {~x} such that for any member of the interval matrix, the eigenvector solution to the problem is a member of the solution set. Thus, the solution to the interval eigenvalue problem for each eigenvector is:
4.3. INTERVAL STIFFNESS MATRIX
The system’s global stiffness can be viewed as a summation of the element contributions to the global stiffness matrix:
n
i=1
where [ Li ] is the element Boolean connectivity matrix and [Ki ] is the element stiffness matrix in the global coordinate system. Considering the presence of uncertainty in the stiffness properties, the non-deterministic element elastic stiffness matrix is expressed as:
~
in which, [li ,ui ] is an interval number that pre-multiplies the deterministic element stiffness matrix. This procedure preserves the physical and mathematical characteristics of the stiffness matrix.
Therefore, the system’s global stiffness matrix in the presence of any uncertainty is the linear summation of the contributions of non-deterministic interval element stiffness matrices:
,ui ])[Li ][Ki ][Li ] =∑
i=1i=1
 in which, [Ki ] is the deterministic element elastic stiffness contribution to the global stiffness matrix.
in which, [Ki ] is the deterministic element elastic stiffness contribution to the global stiffness matrix.
4.4. INTERVAL EIGENVALUE PROBLEM FOR STATICS
The interval eigenvalue problem for a structure with stiffness properties expressed as interval values is:
[K~]{Ï•~} = (λ~){Ï•~} (17)
Substituting Eq.(16) in Eq.(17):
]){Ï•} = (λ){Ï•
i=1
This interval eigenvalue problem can be transformed to a pseudo-deterministic eigenvalue problem subjected to a matrix perturbation. Introducing the central and radial (perturbation) stiffness matrices as:
i 1
 [K~R ] =∑i=n1 (εi )(ui 2−li )[Ki ] , εi =[−1,1] (20)
[K~R ] =∑i=n1 (εi )(ui 2−li )[Ki ] , εi =[−1,1] (20)
Using Eqs. (19,20), the non-deterministic interval eigenpair problem, Eq.(18), becomes:
Hence, the determination of bounds on eigenvalues and bounds on eigenvectors of a stiffness matrix in the presence of uncertainty is mathematically interpreted as an eigenvalue problem on a
~ central stiffness matrix ([KC ]) that is subjected to a radial perturbation stiffness matrix ([KR ]).
This perturbation is in fact, a linear summation of non-negative definite deterministic element stiffness contribution matrices that are scaled with bounded real numbers(εi ) .
5. Solution
5.1. BOUNDS ON EIGENVALUES
The following concepts must be considered in order to bound the non-deterministic interval eigenvalue problem, Eq.(21). The classical linear eigenpair problem for a symmetric matrix is:
with the solution of real eigenvalues (λ1 ≤λ2 ≤ … ≤λn ) and corresponding eigenvectors
( x1, x2,…, xn ). This equation can be transformed into a ratio of quadratics known as the Rayleigh quotient:
R(x) =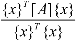 (23)
(23)
The Rayleigh quotient for a symmetric matrix is bounded between the smallest and the largest eigenvalues (Bellman 1960 and Strang 1976).
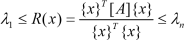 (24)
(24)
Thus, the first eigenvalue (λ1) can be obtained by performing an unconstrained minimization on the scalar-valued function of Rayleigh quotient:
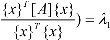
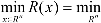 ( (25)
( (25)
x∈
For finding the next eigenvalues, the concept of maximin characterization can be used. This concept obtains the kth eigenvalue by imposing (k-1) constraints on the minimization of the Rayleigh quotient (Bellman 1960 and Strang 1976):
λk = max[minR(x)]
(subject to constrains(xT zi = 0),i =1,…k −1,k ≥ 2 ) (26)
5.1.1. Bounding the Eigenvalues for Statics
Using the concepts of minimum and maximin characterizations of eigenvalues for symmetric matrices, the solution to the interval eigenvalue problem for the eigenvalues of a system with uncertainty in the stiffness characteristics (Eq.(21)) for the first eigenvalue can be shown as:
n
x∈Rn{x}T {x}
for the next eigenvalues:
~{x}T [K~]{x}{x}T ([K ]+[K~ ]){x}
5.1.2. Deterministic Eigenvalue Problems for Bounding Eigenvalues in Statics
Substituting and expanding the right-hand side terms of Eqs. (27,28):
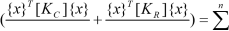
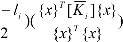
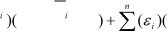

 ~T [K ]{x}~ui
~T [K ]{x}~ui
(li +u{x}
(29)

 Since the matrix [Ki ] is non-negative definite, the term (
Since the matrix [Ki ] is non-negative definite, the term (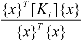 ) is non-negative.
) is non-negative.
Therefore, using the monotonic behavior of eigenvalues for symmetric matrices, the upper bounds on the eigenvalues in Eqs.(19,20) are obtained by considering maximum values of interval coefficients of uncertainty (ε~i = [−1,1]), ((εi )max = 1), for all elements in the radial perturbation matrix.
Similarly, the lower bounds on the eigenvalues are obtained by considering minimum values of those coefficients, ((εi )min =−1) , for all elements in the radial perturbation matrix. Also, it can be observed that any other element stiffness selected from the interval set will yield eigenvalues between the upper and lower bounds. This imonotonic behavior of eigenvalues can also be used for parameterization purposes.
Using these concepts, the deterministic eigenvalue problems corresponding to the maximum and minimum eigenvalues are obtained (Modares and Mullen 2004) as:
n
n
|
5.2. BOUNDS ON EIGENVECTORS 5.2.1. Invariant Subspace The subspace χ is defined to be an invariant subspace of matrix [A] if: |
|
|
Aχ⊂χ |
(32) |
Equivalently, if χ is an invariant subspace of [A]n–n and also, columns of [X1]n–m form a basis forχ, then there is a unique matrix [L1]m–m such that:
The matrix [L1 ] is the representation of [A] on χ with respect to the basis [X1] and the eigenvalues of [L1] are a subset of eigenvalues of [A]. Therefore, for the invariant subspace,
({v},λ) is an eigenpair of [L1] if and only if ({[X1]{v}},λ) is an eigenpair of [A].
5.2.2. Theorem of Invariant Subspaces
For a real symmetric matrix [A], considering the subspace χ with the linearly independent columns of [X1] forming a basis for χ and the linearly independent columns of [X2] spanning the complementary subspace χ⊥ , then, χ is an invariant subspace of [A] iff:
Therefore, invoking this condition and postulating the definition of invariant subspaces, the symmetric matrix [A] can be reduced to a diagonalized form using a unitary similarity transformation as:
|
[X1X2]T [A][X1X2] = ⎢⎡[X1]TT[[AA][][XX11]] ⎣[X2] where [Li ] =[Xi ]T [A][Xi ], i =1,2. 5.2.3. Simple Invariant Subspace |
[X1]T [A][X2]⎤ ⎡[L1] [X2]T [A][X2]⎥⎦= ⎢⎣[0] |
[0] ⎤ [L2]⎥⎦ |
(35) |
An invariant subspace is simple if the eigenvalues of its representation [L1] are distinct from other eigenvalues of [A]. Thus, using the reduced form of [A] with respect to the unitary matrix
[[X1][X2]], χ is a simple invariant subspace if the eigenvalues of [L1] and [L2] are distinct:
5.2.4. Perturbed Eigenvector
Considering the column spaces of [X1] and [X2] to span two complementary simple invariant subspaces, the perturbed orthogonal subspaces are defined as:
|
[Xˆ1] =[X1]+[X 2 ][P] |
(37) |
|
[Xˆ 2 ] =[X 2]−[X1][P]T |
(38) |
in which [P] is a matrix to be determined.
Thus, each perturbed subspace is defined as a summation of the exact subspace and the contribution of the complementary subspace. Considering a symmetric perturbation[E] , the perturbed matrix is defined as:
Applying the theorem of invariant subspaces for perturbed matrix and perturbed subspaces, and linearizing due to a small perturbation compared to the unperturbed matrix, Eq.(34) is rewritten as:
This perturbation problem is an equation for unknown [P] in the form of a Sylvester’s equation in which, the uniqueness of the solution is guaranteed by the existence of simple perturbed invariant subspaces.
Finally, specializing the result for one eigenvector and solving the above equation, the perturbed eigenvector is (Stewart and Sun 1990):
|
{xˆ1} = {x1}+[X 2 ](λ1[I]−[L2 ])−1[X 2 ]T [E]{x1} 5.2.5 Bounding Eigenvectors for Statics For the perturbed eigenvalue problem for statics, Eq.(21), the error matrix is: |
(41) |
|
~nu
|
(42) |
i=12
Using the error matrix in eigenvector perturbation equation for the first eigenvector, Eq.(33) the perturbed eigenvector is:
in which, {Ï•1}is the first eigenvector, (λ1) is the first eigenvalue, [Φ2 ] is the matrix of remaining eigenvectors and [Λ2 ] is the diagonal matrix of remaining eigenvalues obtained from the deterministic eigenvalue problem. Eq.(30,31 and 43) is used to calculate the bounds on interval eigenvalues and interval eigenvectors in the response equation, Eq.(9).
In order to attain sharper results, the functional dependency of intervals in direct interval multiplications in Eq.(9) is considered. Also, input intervals are subdivided and the union of responses of subset results is obtained.
6. Numerical Example Problem
The bounds on the static response for a 2-D statically indeterminate truss with interval uncertainty present in the modulus of elasticity of each element are determined (Figure 2). The crosssectional area A, the length for horizontal and vertical members L , the Young’s moduli E for all
~
elements are E = ([0.99,1.01])E .
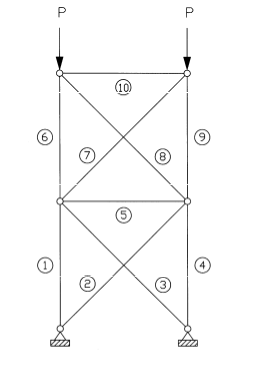
Figure 2. The structure of 2-D truss
The problem is solved using the method presented in this work. The functional dependency of intervals in the response equation is considered. A hundred-segment subdivision of input intervals is performed and the union of responses is obtained. For comparison, an exact combinatorial analysis has performed which considers lower and upper values of uncertainty for each element i.e. solving (2n = 210 =1024 ) deterministic problems.
The static analysis results obtained by the present method and the brute force combination solution for the vertical displacement of the top nodes in are summarized Table (1).
|
Lower Bound Present Method |
Lower Bound Combination Method |
Upper Bound Combination Method |
Upper Bound Present Method |
Error % |
|
|
U
⎜⎟ ⎠AE ⎠|
-1.6265 |
-1.6244 |
-1.5859 |
-1.5838 |
% 0.12 |
Table1. Bounds on Vertical Displacement of Top Nodes
The results show that the proposed robust method yields nearly sharp results in a computationally efficient manner as well as preserving the system’s physics.
4.Conclusions
A finite-element based method for static analysis of structural systems with interval uncertainty in mechanical properties is presented.
This method proposes an interval eigenvalue decomposition of stiffness matrix. By obtaining the exact bounds on the eigenvalues and nearly sharp bounds on the eigenvectors, the proposed method is capable to obtain the nearly sharp bounds on the structure’s static response.
Some conservative overestimation in response occurs that can be attributed to the linearization in formation of bounds of eigenvectors and also, the functional dependency of intervals in the dynamic response formulation.
This method is computationally feasible and it shows that the bounds on the static response can be obtained without combinatorial or Monte-Carlo simulation procedures.
This computational efficiency of the proposed method makes it attractive to introduce uncertainty into structural static analysis and design. While this methodology is shown for structural systems, its extension to various mechanics problems is straightforward.
References
Bellman, R. Introduction to Matrix Analysis, McGraw-Hill, New York 1960.
Dief, A., Advanced Matrix theory for Scientists and Engineers, pp.262-281. Abacus Press 1991.
Hollot, C. and A. Bartlett. On the eigenvalues of interval matrices, Technical Report, Department of Electrical and Computer Engineering, University of Massachusetts, Amherst, MA 1987.
Modares, M. and R. L. Mullen. Free Vibration of Structures with Interval Uncertainty. 9th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliability 2004.
Moore, R. E. Interval Analysis. Prentice Hall, Englewood, NJ 1966.
Muhanna, R. L. and R. L. Mullen. Uncertainty in Mechanics Problems-Interval-Based Approach. Journal of Engineering Mechanics June-2001, pp.557-566 2001.
Muhanna, R. L., Zhang H. and R. L. Mullen. Interval Finite Element as a Basis for Generalized Models of Uncertainty in Engineering Mechanics, Reliable Computing, Vol. 13, pp. 173-194, 2007.
Neumaier, A. Interval Methods for Systems of Equations. Cambridge University Press, Cambridge 1990.
Neumaier, A. and A. Pownuk. Linear Systems with Large Uncertainties, with Applications to Truss Structures, Reliable Computing, Vol. 13, pp. 149-172, 2007.
Strang, G. Linear Algebra and its Applications, Massachusetts Institute of Technology, 1976.
Stewart, G.W. and J. Sun. Matrix perturbation theory, Chapter 5. Academic Press, Boston, MA 1990.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal
 {Ï•i}{Ï•i}
{Ï•i}{Ï•i} [E] = [KR ] = (∑(εi )( i − li )[Ki ])
[E] = [KR ] = (∑(εi )( i − li )[Ki ]) ⎛ PL ⎞
⎛ PL ⎞


